Complexité Algorithmique : Notions, Exemples et Importance

Introduction – Complexité algorithmique vs théorie de la complexité

En informatique, l’analyse de la complexité algorithmique consiste à étudier le coût d’exécution d’un algorithme en fonction de la taille de ses données d’entrée. Elle vise à mesurer les ressources nécessaires (temps de calcul, mémoire…) en fonction de n, la taille de l’instance. Par exemple, on pourra exprimer que « cet algorithme nécessite un nombre d’opérations proportionnel à n² ». L’objectif est de pouvoir comparer l’efficacité d’algorithmes différents sans dépendre d’un langage ou d’une machine en particulier. Cette analyse se focalise souvent sur le pire cas (input le plus défavorable) et le comportement asymptotique quand n devient grand. On utilise pour cela des notations mathématiques comme le Grand O (que nous verrons plus loin). Il s’agit donc d’évaluer rigoureusement « combien de temps » ou « combien d’espace mémoire » un algorithme prendra, en fonction de n, lorsque n grandit vers l’infini. Cette démarche permet de comparer l’efficacité de différentes approches et de prévoir leur passage à l’échelle.

Il faut distinguer cela de la théorie de la complexité computationnelle (informatique théorique). La théorie de la complexité ne s’intéresse plus à un algorithme en particulier, mais au problème lui-même : quelle est la difficulté intrinsèque de ce problème ? On cherche à classifier les problèmes (et non les algorithmes individuels) selon les ressources minimales nécessaires pour les résoudre. Par exemple, on distingue la classe des problèmes résolus en temps polynomial (classe P) de ceux pour lesquels aucun algorithme polynomial n’est connu (classe NP etc.). Cette théorie introduit des classes de complexité et étudie leurs relations (fameuse question P vs NP, etc.). Complexité algorithmique et complexité computationnelle sont liées, mais à des échelles différentes : la première analyse des algorithmes concrets, la seconde classe des problèmes abstraits par difficulté. Dans cet article, nous nous concentrerons sur l’analyse de la complexité des algorithmes et sur les outils pour l’estimer.

Complexité en temps et en espace

Deux des mesures de complexité les plus courantes sont la complexité en temps et la complexité en espace. La complexité en temps d’un algorithme est une fonction qui associe à chaque taille d’entrée n le temps de calcul nécessaire (typiquement le nombre d’opérations élémentaires effectuées). On exprime ce temps de calcul de manière indépendante de la machine utilisée, en comptant par exemple les itérations, les comparaisons ou toute opération significative. Par convention, on évalue souvent le temps d’exécution dans le pire cas, c’est-à-dire le nombre maximal d’étapes que l’algorithme effectuera pour une entrée de taille n donnée. (On peut également étudier le meilleur cas ou le cas moyen, mais le pire cas donne une garantie supérieure sur le comportement de l’algorithme.) Lorsque n devient très grand, on s’intéresse surtout à l’ordre de grandeur asymptotique du temps d’exécution plutôt qu’aux constantes multiplicatives ; cela permet de comparer l’efficacité de deux algorithmes sur le long terme.

De même, la complexité en espace mesure la quantité de mémoire utilisée par un algorithme en fonction de la taille de l’entrée. On évalue typiquement le nombre maximal de cases mémoire occupées simultanément durant l’exécution (en plus de l’entrée elle-même). Par exemple, un algorithme de tri en place qui ne nécessite que quelques variables temporaires a une complexité en espace faible (constante), tandis qu’un algorithme qui doit copier ses données aura une complexité en espace linéaire en la taille de celles-ci. Comme pour le temps, on considère souvent le pire cas et le comportement asymptotique. Il est important de noter que temps et espace peuvent être en compromis : certains algorithmes utilisent plus de mémoire pour gagner du temps, et inversement. Idéalement, on cherche des solutions économes à la fois en temps d’exécution et en utilisation mémoire.

En résumé, la complexité en temps nous indique combien de temps de calcul demande un algorithme en fonction de n, et la complexité en espace indique combien de mémoire il requiert. Ces deux métriques aident à anticiper si un algorithme sera praticable sur de grandes entrées (par exemple, un programme en temps linéaire sera faisable sur des millions de données, tandis qu’un programme en temps exponentiel ne le sera plus au-delà de quelques dizaines d’éléments).

Notations asymptotiques : O, Ω, Θ

Pour exprimer de façon rigoureuse la complexité en fonction de n, on utilise les notations asymptotiques : principalement O (« grand O »), Ω (oméga) et Θ (thêta). Celles-ci permettent de donner des bornes sur la croissance d’une fonction lorsque n tend vers l’infini, en ignorant les constantes multiplicatives et les termes de plus faible ordre. Intuitivement, on cherche à catégoriser une fonction de complexité (par exemple T(n)) par rapport à une fonction de référence plus simple (par exemple n, n², n log n, etc.).

Notation O (borne supérieure) : On dit que f(n) = O(g(n)) si f(n) croît au plus aussi vite qu’une constante fois g(n) lorsque n est grand. Plus formellement, il existe une constante positive c et un rang n₀ tels que pour tout n ≥ n₀, on ait f(n) ≤ c · g(n). Cette notation fournit donc une borne supérieure asymptotique – elle garantit que, pour n suffisamment grand, f(n) ne dépasse pas g(n) à un facteur constant près. En complexité, O(g(n)) désigne l’ensemble des fonctions qui sont au plus de l’ordre de g(n). Par exemple, si un algorithme effectue au plus 3n² + 5n + 2 opérations, on dira qu’il est O(n²) (car pour n grand, 3n² + 5n + 2 est dominé par une constante fois n²). La notation O sert surtout à exprimer le pire cas d’un algorithme : « cet algorithme est O(n²) » signifie que son temps d’exécution croît au plus comme le carré de n. Important : dire « f(n) est O(g(n)) » n’exclut pas que f(n) puisse être bien plus petit que g(n) pour de grandes valeurs de n (c’est juste une majoration).
Notation Ω (borne inférieure) : De manière duale, on dit que f(n) = Ω(g(n)) si f(n) croît au moins aussi vite (à une constante près) que g(n) lorsque n est grand. Formellement, il existe des constantes c’ > 0 et n₀ telles que pour tout n ≥ n₀, f(n) ≥ c’ · g(n). La notation Ω donne une borne inférieure asymptotique – elle assure qu’asymptotiquement, f(n) ne peut pas croître plus lentement que g(n). En termes de complexité, Ω(g(n)) est souvent utilisée pour le meilleur cas d’un algorithme ou pour affirmer qu’un problème nécessite au moins un certain coût. Par exemple, la recherche séquentielle dans une liste non triée est Ω(n) car il faut au minimum parcourir n éléments dans le pire des cas pour être sûr de trouver une valeur donnée (même si en moyenne on peut parfois s’arrêter plus tôt).
Notation Θ (borne équivalente, croissance « serrée ») : On dit que f(n) = Θ(g(n)) s’il existe deux constantes c₁, c₂ > 0 et n₀ tels que c₁·g(n) ≤ f(n) ≤ c₂·g(n) pour tout n ≥ n₀. Autrement dit, f(n) est à la fois O(g(n)) et Ω(g(n)). La notation Θ décrit une croissance asymptotique équivalente : f(n) et g(n) sont du même ordre de grandeur asymptotique. C’est la notion de borne serrée. Par exemple, si l’on a f(n) = 2n² + 3n + 1, alors f(n) = Θ(n²) (car cette fonction est bornée à la fois au-dessus et en dessous par une constante fois n² pour n grand). En complexité des algorithmes, établir que le temps d’un algorithme est Θ(g(n)) signifie qu’on a cerné précisément son ordre de croissance dominant. Si de plus un problème admet un algorithme en O(g(n)) et qu’on peut prouver qu’aucun algorithme ne peut faire mieux que Ω(g(n)), alors g(n) est l’ordre de complexité optimal du problème.

En résumé, O donne une borne haute (au-dessus), Ω une borne basse (en dessous), et Θ indique que la fonction de coût est encadrée des deux côtés par la même forme (croissance équivalente). Dans la pratique, on utilise le plus souvent le Grand O pour exprimer le temps de calcul maximal d’un algorithme. Par exemple : « l’algorithme de tri par insertion est O(n²) dans le pire cas ». On peut parfois préciser qu’il est aussi Ω(n) dans le meilleur cas (données déjà triées), etc. Ces notations asymptotiques permettent d’ignorer les constantes multiplicatives et les termes sub-dominants, ce qui donne une vision claire de l’évolutivité d’un algorithme lorsque la taille des données augmente.

Exemples concrets de complexité (avec code)

Après la théorie, passons à la pratique : examinons quelques algorithmes classiques et analysons leur complexité. Nous présenterons pour chacun un extrait de code en Python et expliquerons comment le nombre d’opérations évolue en fonction de n. Ces exemples concrets vont illustrer les notions de complexité linéaire, logarithmique, quadratique, cubique, etc., que nous avons évoquées.

Recherche linéaire – Complexité O(n)

Commençons par un algorithme simple : la recherche linéaire (ou séquentielle) d’une valeur dans un tableau non trié. L’idée est de parcourir la liste élément par élément jusqu’à trouver l’élément cible (ou arriver à la fin sans le trouver). Voici une implémentation Python de la recherche linéaire :

def recherche_lineaire(tableau, cible):
    for i, element in enumerate(tableau):
        if element == cible:
            return i   # renvoie l'indice où la cible est trouvée
    return -1          # renvoie -1 si la cible n'est pas présente

Dans le pire des cas (par exemple, si la valeur recherchée est absente du tableau ou se trouve en dernière position), cette fonction parcourra toute la liste de longueur n. Le nombre de comparaisons sera alors proportionnel à n. On peut donc dire que la recherche linéaire a une complexité en temps O(n) dans le pire cas. En effet, le temps d’exécution croît linéairement avec le nombre d’éléments : si on double la taille de la liste, le temps de recherche maximal double approximativement. À l’inverse, le meilleur cas serait que la valeur soit trouvée au tout début (une seule comparaison), soit un temps constant O(1). Mais sans information particulière sur la distribution des données, on retient le pire cas linéaire. Pour donner un ordre d’idée, chercher un nom dans un annuaire de 30 000 contacts en parcours séquentiel nécessitera au pire 30 000 opérations de comparaison – ce qui est faisable, mais si l’annuaire passe à des millions de contacts, cela devient beaucoup plus long.

Recherche dichotomique – Complexité O(log n)

Supposons maintenant que l’on dispose d’une liste triée. Peut-on chercher une valeur plus efficacement que de tout parcourir ? Oui, grâce à la recherche dichotomique (aussi appelée recherche binaire). Le principe est de comparer la valeur cherchée à l’élément du milieu du tableau : si la valeur cible est plus petite, on sait qu’elle se trouve dans la première moitié (puisque le tableau est trié) ; si elle est plus grande, on ira chercher dans la seconde moitié. En répétant ce découpage en deux, on réduit drastiquement le nombre de comparaisons. Voici une implémentation en Python :

def recherche_dichotomique(tableau, cible):
    gauche = 0
    droite = len(tableau) - 1
    while gauche <= droite:
        milieu = (gauche + droite) // 2
        if tableau[milieu] == cible:
            return milieu   # trouvé à l'indice milieu
        elif tableau[milieu] < cible:
            gauche = milieu + 1   # chercher dans la moitié droite
        else:
            droite = milieu - 1   # chercher dans la moitié gauche
    return -1  # non trouvé

Dans cette boucle, à chaque itération on divise par deux la portion de tableau dans laquelle la valeur peut se trouver. On passe ainsi d’un espace de recherche de n éléments à n/2, puis n/4, etc., jusqu’à éventuellement trouver la valeur ou réduire l’espace à zéro. Le nombre d’itérations avant d’arrêter est d’environ log₂(n) (logarithme en base 2 de n) dans le pire des cas. Autrement dit, la complexité de cet algorithme en temps est O(log n). Pour reprendre l’exemple de l’annuaire de 30 000 noms : une recherche dichotomique trouvera le nom en au plus 15 comparaisons environ (puisque 2^15 ≈ 32 768), contre 30 000 comparaisons pour la recherche linéaire – un gain spectaculaire.

Ci-dessous, une illustration montre comment la recherche dichotomique procède par divisions successives de l’espace de recherche : à chaque étape, la moitié des éléments est éliminée.

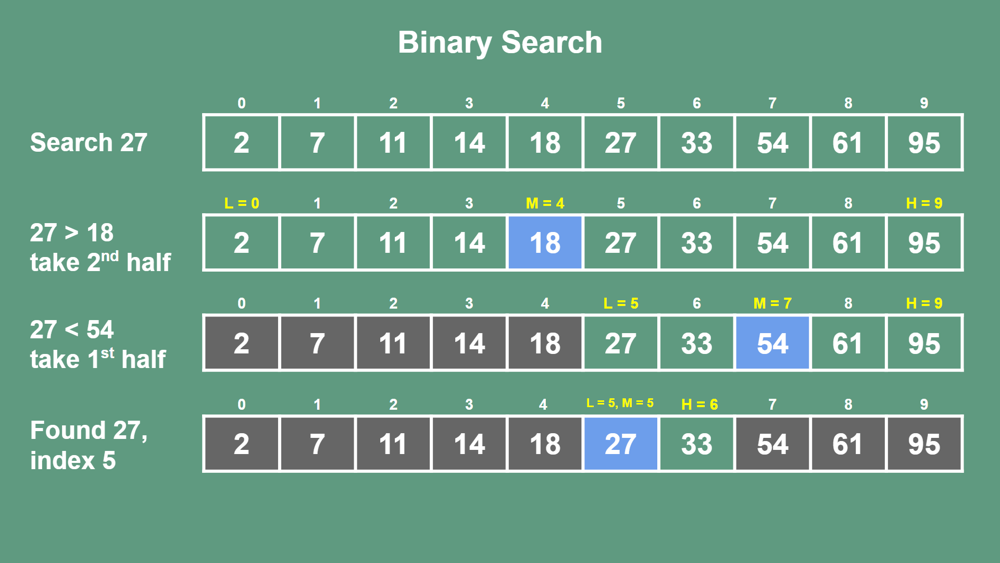
Exemple visuel de la recherche dichotomique (binary search) qui réduit de moitié l’espace de recherche à chaque étape. Les tableaux représentent la portion restante à chaque itération, jusqu’à trouver la valeur cible (27) à l’indice 5.

Ainsi, la recherche dichotomique est extrêmement efficace sur de grands volumes de données triées. Cependant, elle nécessite impérativement que la liste soit triée au préalable (ce qui, en soi, peut coûter du temps). Si les données ne sont pas triées, on ne peut pas éliminer la moitié en un test, et la recherche séquentielle O(n) reste la seule solution générale.

Boucles imbriquées – Complexité O(n²)

Considérons un algorithme dont les étapes comportent deux boucles imbriquées parcourant chacune n éléments. Par exemple, une double boucle qui compare tous les couples d’éléments dans un tableau, ou qui génère une table de multiplication n × n. Voici un petit exemple en Python :

def operations_quadratiques(n):
    compteur = 0
    for i in range(n):
        for j in range(n):
            compteur += 1   # opération constante O(1) dans la boucle interne
    return compteur

Cette fonction effectue un incrément compteur += 1 pour chaque paire (i, j) avec i allant de 0 à n-1 et j de 0 à n-1. Il y a exactement n × n itérations au total, soit n² opérations élémentaires. On en déduit que la complexité en temps est O(n²) (croissance quadratique). En effet, le nombre d’opérations croît comme le carré de n. Pour n = 100, on effectue 10 000 incréments ; pour n = 1000, un million d’incréments, etc. De manière générale, si l’on double n, le temps d’exécution est multiplié par ~4 (2²).

De nombreux algorithmes ont un comportement quadratique, par exemple le tri à bulles (qui compare tous les couples d’éléments adjacents) ou le tri par insertion dans le pire cas. Au-delà de quelques milliers d’éléments, une complexité O(n²) peut devenir problématique, car le temps de calcul augmente très vite. Par exemple, un algorithme en n² qui prend 1 seconde pour n = 10 000 éléments en prendra environ 4 secondes pour n = 20 000, ~100 secondes pour n = 100 000, et deviendra carrément impraticable pour n = 1 000 000 (un million) d’éléments (où n² = 10^12 opérations). D’où l’importance de chercher des algorithmes plus efficients lorsque n devient grand.

Multiplication de matrices – O(n³) vs algorithme de Strassen (~O(n^2.8))

Pour illustrer une complexité cubique O(n³) et voir comment on peut parfois la réduire, penchons-nous sur la multiplication de matrices carrées de taille n × n. L’algorithme standard (appris en mathématiques) multiplie deux matrices A et B en calculant tous les produits scalaires entre lignes de A et colonnes de B. En pseudo-code, cela donne trois boucles imbriquées :

def multiplication_matrices(A, B):
    n = len(A)
    C = [[0] * n for _ in range(n)]
    for i in range(n):
        for j in range(n):
            for k in range(n):
                C[i][j] += A[i][k] * B[k][j]
    return C

Ici, les indices i et j parcourent respectivement les lignes et colonnes du résultat C, et la boucle k accumule le produit des éléments correspondants de la i-ème ligne de A et de la j-ème colonne de B. Le nombre d’opérations élémentaires (multiplications et additions) effectuées est d’environ n × n × n = n³. Donc la complexité en temps de l’algorithme naïf de multiplication de deux matrices de dimension n est Θ(n³). Pour donner un ordre de grandeur, multiplier deux matrices 100×100 nécessite de l’ordre de 1 000 000 d’opérations, et des matrices 1000×1000 en nécessitent 1 000 000 000 (un milliard). On comprend qu’améliorer cet ordre de complexité serait précieux pour le calcul scientifique ou le traitement d’images par exemple, où les matrices peuvent être très grandes.

De fait, il existe des algorithmes plus rapides que Θ(n³) pour la multiplication matricielle. Le premier a été découvert par Volker Strassen en 1969 : l’algorithme de Strassen utilise une approche récursive ingénieuse. Son idée est de découper les matrices en sous-matrices (de taille n/2 × n/2) et de réduire le nombre de multiplications nécessaires en combinant astucieusement les résultats. Alors que l’approche naïve multiplie 8 sous-matrices (pour calculer les 4 blocs du résultat), Strassen parvient à n’en multiplier que 7, au prix de quelques additions supplémentaires. Ce gain de 1 multiplication peut paraître anodin, mais en réappliquant la méthode récursivement, le nombre total d’opérations suit une récurrence : T(n) = 7 T(n/2) + O(n²) (les O(n²) proviennent des additions de matrices). Résoudre cette récurrence (par le Master Theorem, que l’on verra plus loin) donne un ordre asymptotique d’environ O(n^log27), soit O(n^2.8074…). Ainsi, l’algorithme de Strassen a une complexité inférieure à n³. En pratique, cela signifie que pour des matrices très grandes, Strassen sera plus rapide que l’algorithme classique. Par exemple, pour n = 1024, n³ ≈ 1,07×10^9 opérations tandis que n^2.807 ≈ 4.7×10^8* : presque deux fois moins.

L’algorithme de Strassen marque le début d’une longue série de recherches en algorithmique. Depuis 1969, d’autres méthodes de multiplication de matrices encore plus rapides (mais de plus en plus complexes) ont été découvertes. L’exposant de complexité a ainsi été progressivement abaissé : 2.80, 2.78, 2.67, … jusqu’à environ 2.37 aujourd’hui. Autrement dit, on sait théoriquement multiplier deux matrices en O(n^2.37) environ, grâce à des algorithmes très sophistiqués. Cependant, ces améliorations extrêmes – parfois qualifiées d’algorithmes galactiques – ne sont pas utilisées en pratique. En effet, ils ne deviennent avantageux qu’à des tailles de matrices astronomiquement grandes, et leur overhead (constantes cachées, complexité d’implémentation) les rend plus lents sur les matrices de taille courante. En pratique, l’algorithme de Strassen lui-même n’est utile que pour des matrices au-delà d’un certain seuil (typiquement quelques centaines ou milliers) ; en-deçà, le classique triple boucle peut être plus rapide à cause des optimisations CPU/cache. Cet exemple illustre qu’une meilleure complexité asymptotique n’est pas toujours synonyme de meilleure performance réelle sur des inputs de taille modérée – mais à très grande échelle, elle finit par l’emporter. Quoi qu’il en soit, la découverte de Strassen fut fondamentale car elle a démontré que la borne n³ n’était pas une barrière absolue, ouvrant tout un champ de recherche en algorithmique.

Présentation du Master Theorem (Théorème du Maître)

La résolution de la récurrence de l’algorithme de Strassen ci-dessus nous amène à un outil précieux en analyse d’algorithmes : le Master Theorem (ou théorème du maître). Il s’agit d’un théorème qui donne, sans effort de calcul itératif, l’ordre de grandeur asymptotique des solutions de récurrences divide-and-conquer courantes. De nombreux algorithmes récursifs divisent en effet le problème en plusieurs sous-problèmes plus petits. Le Master Theorem considère les récurrences de la forme :

T(n)=a T ⁣(nb)+f(n),T(n) = a \; T\!\Big(\frac{n}{b}\Big) + f(n),

où a ≥ 1 est le nombre de sous-problèmes, b > 1 le facteur de réduction de la taille (chaque sous-problème a une taille ~n/b), et f(n) le coût hors récursion (temps pour diviser/recombiner les sous-problèmes). Intuitivement, on a un arbre de récursion de hauteur ~log_b(n) où à chaque niveau les a^k appels de ce niveau traitent des problèmes de taille n/b^k. Le théorème du maître fournit une solution asymptotique T(n) = Θ(g(n)) selon la comparaison entre f(n) et nlogba, qui représente (à un facteur près) le coût total de tous les sous-problèmes. On définit pour cela l’exposant critique c = log_b(a) (aussi noté ccritique). Trois cas se présentent :

Cas 1 : f(n) est « petit » par rapport à n^c. Plus précisément, si f(n) = O(nc – ε) pour une certaine constante ε > 0 (c’est-à-dire f(n) est asymptotiquement plus petit que n^c à un facteur polynomial près), alors les sous-problèmes dominent le coût et on a :

T(n)=Θ(nc).T(n) = Θ\big(n^c\big).

(Intuition : le travail est dominé par les feuilles de l’arbre de récursion, donc équivalent au coût des alog_b n = n^c sous-problèmes de taille 1.)

Cas 2 : f(n) est de même ordre que n^c (à un facteur polylog près). Si f(n) = Θ(n^c · (\log n)^k) pour un certain k ≥ 0 (incluant le cas f(n) = Θ(n^c)), alors les coûts se répartissent équilibrés entre la partie récursive et la partie f(n), et on obtient :

T(n)=Θ(nc(log⁡n) k+1).T(n) = Θ\big(n^c (\log n)^{\,k+1}\big).

(Intuition : le travail total est la somme de contributions équivalentes à chaque niveau de l’arbre, sur ~log n niveaux.)

Cas 3 : f(n) est « grand » par rapport à n^c. Plus formellement, si f(n) = Ω(nc + ε) pour une constante ε > 0 – et sous une condition technique dite de régularité garantissant que f ne croît pas trop plus vite que n^c (condition souvent vérifiée dans les cas usuels) – alors c’est f(n) qui domine et on a :

T(n)=Θ(f(n)).T(n) = Θ\big(f(n)\big).

(Intuition : le coût hors récursion à la racine de l’arbre (et peut-être aux premiers niveaux) l’emporte sur le coût combiné de tous les sous-problèmes.)

En appliquant le Master Theorem, on peut ainsi obtenir directement la complexité asymptotique sans dérouler la récurrence niveau par niveau. Reprenons quelques exemples classiques d’algorithmes divide-and-conquer : le tri fusion s’analyse avec a=2, b=2, f(n)=Θ(n) (fusion de deux tableaux triés) ; ici c = log₂2 = 1 et f(n) est Θ(n^1), donc cas 2 avec k=0 : on obtient T(n) = Θ(n · log n), bien connu pour le merge sort. Pour l’algorithme de Strassen vu plus haut, a=7, b=2, c = log₂7 ≈ 2.807, et f(n)=O(n²) était O(n^{c – ε}) (car 2 < 2.807), on est dans le cas 1, d’où T(n) = Θ(n^c) = Θ(n^2.807), cohérent avec le résultat annoncé. Un dernier exemple : la recherche dichotomique peut s’exprimer par T(n) = T(n/2) + Θ(1) (une comparaison + orientation vers une moitié) ; ici a=1, b=2, c=log₂1 = 0, et f(n)=Θ(1) = Θ(n^0) donc cas 2 (avec k=0) : on retrouve T(n) = Θ((n^0) · log n) = Θ(log n).

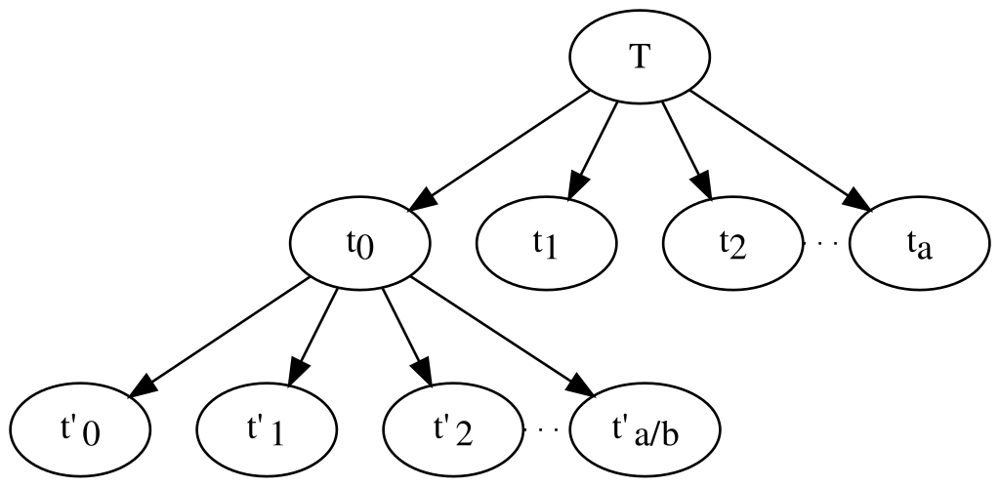
Visuellement, on peut interpréter le Master Theorem à l’aide de l’arbre de récursion évoqué :

Schéma d’un arbre de récursion pour un algorithme divisant chaque problème en a sous-problèmes de taille ~1/b (ici illustré abstraitement). Le théorème du maître compare le coût total des feuilles (nombre de nœuds terminals ~nlogba) avec le coût total de la racine et des niveaux intermédiaires (par rapport à f(n)).

Le Master Theorem est un outil très pratique pour analyser des algorithmes récursifs comme : tri fusion, tri rapide (quicksort), recherche binaire, exponentiation rapide, algorithms de divide-and-conquer divers (multiplication de grandes entiers, transformée de Fourier rapide, etc.). Il ne couvre pas tous les types de récurrences (certaines nécessitent des variantes ou d’autres méthodes, e.g. méthode d’Akra-Bazzi, résolution par expansion en arbre, etc.), mais dans de nombreux cas courants il permet d’obtenir immédiatement la complexité asymptotique. Il est important de bien identifier a, b et f(n) puis d’appliquer le cas correspondant. Avec un peu de pratique, on développe une intuition : par exemple, si f(n) est n^c polynomiale et domine la formule de recombinaison, on pressent directement un cas 3 (coût dominé par f(n)); si f(n) est linéaire et qu’on a deux sous-appels moitié taille, on anticipe un cas 2 donnant n log n, etc. Cette capacité à estimer rapidement la complexité vient avec l’habitude et grâce à des outils comme le Master Theorem.

Comparatif des ordres de complexité

La complexité d’un algorithme influe directement sur son temps d’exécution et sa faisabilité pratique, en particulier lorsque la taille des données augmente. Il est instructif de comparer la croissance des principales fonctions de complexité courantes. Le graphique ci-dessous illustre l’augmentation du coût (en nombre d’opérations arbitraires) en fonction de n pour différentes classes de complexité : constante O(1), logarithmique O(log n), linéaire O(n), quasi-linéaire O(n log n), quadratique O(n²) et exponentielle O(2^n).

Croissance comparée (échelle linéaire) de différentes fonctions de complexité en fonction de n (jusqu’à 100). On observe que les fonctions linéaire O(n) (courbe rouge) et n log n O(n log n) (rose) croissent modérément, alors que la fonction quadratique O(n^2) (bleu clair) monte bien plus rapidement. La fonction exponentielle O(2^n) (pointillés violets) explose littéralement : même pour n = 20 elle dépasse 1 000 000 (ce qui la rend impraticable au-delà de très petites entrées).

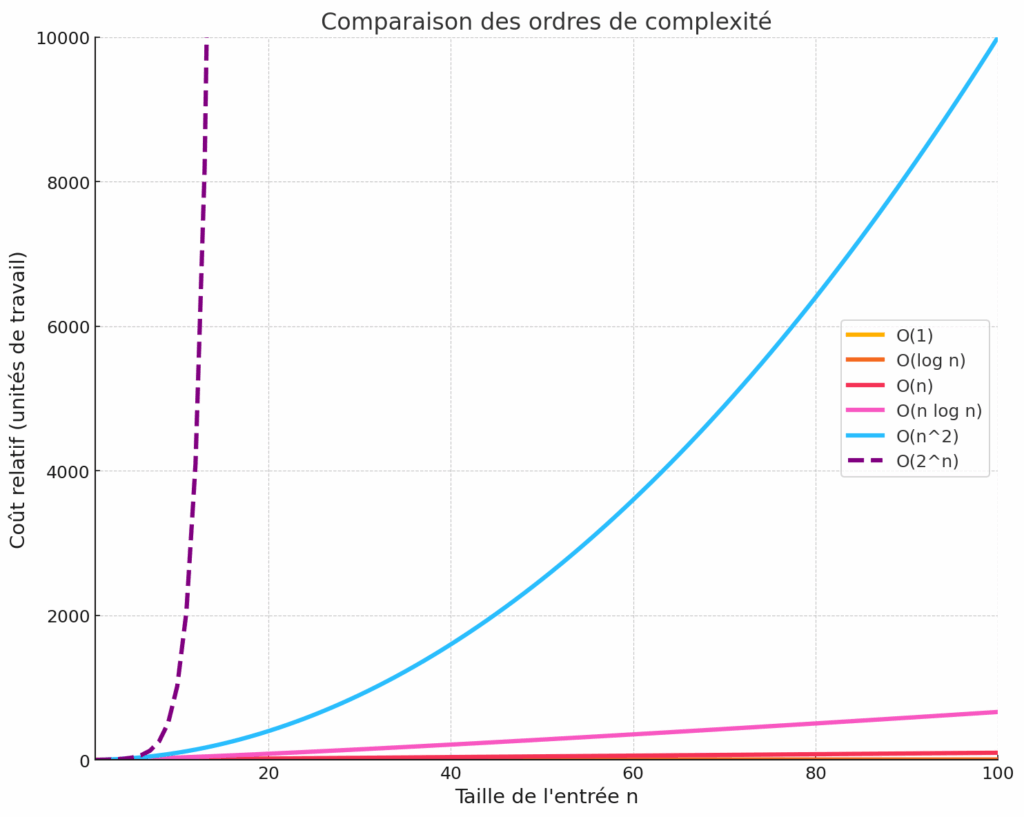
On constate sur ce visuel que :

Une complexité constante O(1) (courbe orange, confondue avec l’axe des x sur le graphe) est indépendante de n – c’est l’idéal, mais rare sur des problèmes non triviaux. Par exemple accéder à un élément dans un tableau par son index est une opération O(1).
Une complexité logarithmique O(log n) (courbe orange foncé) croît très lentement : doubler n n’augmente le coût que de façon additive. La recherche dichotomique en est un exemple typique. Pour n = 1 000 000, log₂(n) ≈ 20 : un algorithme O(log n) ferait environ 20 étapes, ce qui est excellent.
Une complexité linéaire O(n) (courbe rouge) croît proportionnellement : si on double n, le temps double. C’est souvent acceptable pour des n assez grands (par ex., parcourir 1 million d’éléments prend un temps proportionnel à 1 million). De nombreux algorithmes sont linéaires (parcours de liste, somme de n nombres, recherche dans un tableau non trié, etc.).
Une complexité quasi-linéaire O(n log n) (courbe rose) est légèrement plus coûteuse que linéaire : elle ajoute un facteur log. Les meilleurs algorithmes de tri généraux (tri fusion, tri rapide moyen) sont en O(n log n). Pour n = 1 000 000, n log₂ n ≈ 20 000 000 (20 millions), ce qui reste faisable en quelques secondes sur un PC moderne.
Une complexité quadratique O(n²) (courbe bleu clair) devient lourde pour des n élevés. Si on multiplie n par 10, le temps est multiplié par 100. Un algorithme en n² qui traite 10 000 éléments en 1 seconde en mettra 100 secondes pour 100 000 éléments (plus d’une minute), et ainsi de suite. Les double-boucles imbriquées mènent souvent à O(n²). Il faut faire attention dès que n dépasse quelques milliers.
Une complexité exponentielle O(2^n) (pointillés violets) est explosive : le temps de calcul double à chaque élément additionnel. Un algorithme en 2^n est pratiquement inutilisable au-delà de n = 40 ou 50 (2^50 ≈ 1 quadrillion ≈ 10^15 opérations). Des problèmes d’optimisation par force brute (voyageur de commerce, etc.) ou d’énumération exhaustive ont des complexités exponentielles. Il n’est généralement pas envisageable de traiter exhaustivement des grandes instances de tels problèmes – on cherche alors des heuristiques, des approximations, ou on restreint la taille de n.

À titre d’exemple chiffré pour comparer O(n) et O(log n) : pour n = 30 000, une algorithme en O(n) effectuera ~30 000 opérations, alors qu’un algorithme en O(log n) en fera environ log₂(30000) ≈ 15. L’écart se creuse encore plus pour des n plus grands. En revanche, entre un algorithme O(n) et un autre O(n log n), la différence n’est pas flagrante sur des tailles modérées (disons n ≤ quelques milliers), mais devient significative pour des millions d’éléments (le facteur log n commence à peser). Quant aux algorithmes quadratiques ou pires, ils deviennent rapidement prohibitif en temps de calcul dès que n grandit. C’est pourquoi en pratique, un développeur cherchera à éviter les algorithmes exponentiels ou quadratiques sur de grandes entrées, et privilégiera des solutions en temps linéaire ou n log n si possible. Lorsqu’un problème semble nécessiter une complexité exponentielle, cela suggère souvent qu’il appartient à une classe de problèmes intractables (en tout cas à grande échelle) : on entre alors dans le domaine de la complexité computationnelle (problèmes NP-complets, etc., pour lesquels on pense qu’aucune solution polynomialement efficace n’existe).

En résumé, maîtriser la complexité permet de prévoir le comportement d’un algorithme quand les données augmentent et d’adapter ses choix en conséquence. La différence entre un algorithme O(n log n) et O(n²) peut déterminer si une application passe à l’échelle ou s’effondre lorsque n croît. D’où l’importance, pour un informaticien, de bien comprendre ces ordres de grandeur.

Conclusion – L’importance de la complexité en pratique

La complexité algorithmique n’est pas qu’une notion théorique : elle a un impact direct et concret sur les performances des logiciels. En développement, analyser la complexité des différentes solutions possibles permet de choisir l’algorithme le plus adapté à son problème et à ses contraintes. Par exemple, pour manipuler un petit tableau de 100 éléments, un algorithme O(n²) peut très bien suffire et sa simplicité de code peut être un atout. Mais si l’application doit gérer des millions d’enregistrements, il faudra absolument une méthode plus efficiente (O(n log n) ou O(n) selon le cas) faute de quoi le temps de réponse deviendra inacceptable. De même, en algorithmique avancée, comprendre la complexité aide à identifier les goulets d’étranglement et à concentrer les optimisations sur les parties critiques du code.

En pratique, les ingénieurs utilisent l’analyse de complexité conjointement avec des tests empiriques (mesures de temps) pour valider les performances. La complexité donne une tendance asymptotique indépendante du matériel, tandis que les benchmarks mesurent le temps réel en incluant les constantes, effets de cache, etc. Les deux se complètent pour prévoir le comportement d’un programme. Notons aussi que la complexité en espace peut être déterminante : sur des systèmes embarqués à mémoire limitée, un algorithme légèrement plus lent en temps mais bien plus économe en mémoire peut être préféré.

Enfin, l’étude de la complexité sensibilise aux limites de l’informatique. Elle met en lumière des problèmes pour lesquels aucun algorithme efficace n’est connu (par exemple le fameux problème NP-complet du voyageur de commerce qui, en brute force, croît en O(n!)). Elle encourage également la recherche de nouvelles méthodes : c’est en tentant d’améliorer la complexité qu’ont été inventés des algorithmes révolutionnaires (tri rapide, algorithme de Dijkstra, compression de données, etc.). Pour aller plus loin, on pourra consulter des ressources comme le classique “The Art of Computer Programming” de Donald Knuth, qui aborde en profondeur l’analyse des algorithmes et des structures de données, ou encore les nombreux articles et cours en ligne (par ex. sur GeeksforGeeks ou Wikipédia) consacrés aux différents algorithmes et à leur complexité. La plateforme ArXiv regorge également de publications de recherche en algorithmique qui poussent toujours plus loin les frontières (par ex. les dernières avancées sur la multiplication de matrices, la résolution d’instances NP-difficiles, etc.). En somme, la complexité algorithmique est un aspect fondamental de la science informatique : en être conscient et savoir l’estimer donne un véritable pouvoir prédictif et contribue à écrire du code à la fois élégant et efficace, capable de relever les défis des données massives de notre époque.

Sources et pour approfondir :

Wikipédia – Complexité en temps, Complexité en espace, Notation Big O, Théorie de la complexité, etc.. Des articles détaillés couvrent chaque notion présentée.
GeeksforGeeks – Tutoriels en anglais sur l’analyse de complexité et structures de données (ex : “Big-O vs Theta vs Omega Notations”, “Master Theorem” etc.), avec de nombreux exemples de code.
The Art of Computer Programming, vol. 1 (D. Knuth) – Chapitres 1 et 2 sur les algorithmes fondamentaux, contenant une présentation rigoureuse de l’analyse de complexité et de nombreux exemples classiques.
Cormen et al., Introduction to Algorithms – Livre de référence couvrant l’analyse d’algorithmes (contient le Master Theorem, exemples de complexité, etc.).
Ressources en ligne (cours, PDF) – Par ex. le cours “Algorithmique : Notion de complexité” de l’UPMC, ou les notes de Sylvain Perifel, Complexité algorithmique, Ellipses 2014, pour une approche plus mathématique.
Articles de recherche (sur arXiv) – Pour les passionnés, suivre les développements sur des sujets pointus (par ex. l’algorithme de multiplication de matrices de V. Vassilevska Williams, etc.) permet de voir comment on repousse les limites de la complexité dans des domaines spécifiques.

Toutes ces ressources vous permettront d’approfondir vos connaissances et de découvrir de nouveaux exemples. La complexité algorithmique est un domaine riche et en constante évolution : en la maîtrisant, vous acquérez une clé pour concevoir des programmes performants et mieux comprendre ce que la machine peut (ou ne peut pas) accomplir dans un temps donné. Bonne exploration !