Commençons par présenter le neurone formel:
import matplotlib.pyplot as plt
import networkx as nx
Création du graphe
G = nx.DiGraph()
Ajout des nœuds
G.add_node("x1", pos=(0, 1))
G.add_node("x2", pos=(0, -1))
G.add_node("z", pos=(1, 0))
G.add_node("a", pos=(2, 0))
G.add_node("y_pred", pos=(3, 0))
G.add_node("-1", pos=(1, 1))
Ajout des arêtes avec les labels
G.add_edge("x1", "z", weight="w1")
G.add_edge("x2", "z", weight="w2")
G.add_edge("z", "a")
G.add_edge("a", "y_pred")
G.add_edge("-1", "z")
Positions des nœuds
pos = nx.get_node_attributes(G, 'pos')
Dessin du graphe
plt.figure(figsize=(8, 6))
nx.draw(G, pos, with_labels=True, node_size=3000, node_color="white", edgecolors="black", font_size=15)
Dessin des labels sur les arêtes
edge_labels = {('x1', 'z'): 'w1', ('x2', 'z'): 'w2', ('z', 'a'): 'z', ('a', 'y_pred'): 'a', ('-1', 'z'): 'b'}
nx.draw_networkx_edge_labels(G, pos, edge_labels=edge_labels, font_color='red', font_size=15)
Affichage de la formule en bas
plt.text(1.5, -1, r'$z = w_1 x_1 + w_2 x_2 - b$', fontsize=15, ha='center')
plt.axis('off')
plt.show()Code en python pour réaliser ce schéma:
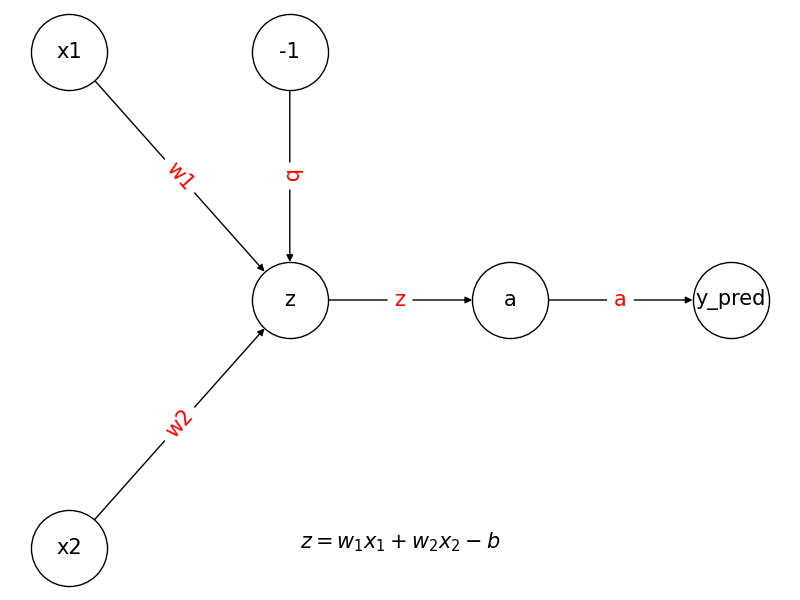
Cette représentation mathématique pensée en 1943 par Warren McCulloch et Walter Pitts est le premier modèle mathématique du neurone biologique.
Les poids w_isont aussi appelés poids synaptique par référence au cerveau humain.
Ce modèle permet de réaliser des opérations de classifications linéaire (frontière de séparation une droite, ou un plan ou bien plus largement un hyperplan en lorsqu’il s’agit de prendre en compte plus de 3 dimensions).
La fonction d’activation utilisé initialement était une variante de la fonction dite de Heavyside , la fonction signe :

Cela permet de fournir en sortie deux résultats: 1 ou -1 et donc d’identifier deux classes différentes.
Il s’agit alors de trouver les poids synaptique permettant d’effectuer correctement la classification en trouvant une frontière de décision, exemple ici pour une porte OR:

Ce neurone formel a ses limites en particuliers il ne peut effectuer qu’une classification linéaire et n’est donc pas capable de représenter une porte XOR (ou exclusif)
Frank Rosenblatt mis au point un algorithme permettant de calculer les poids synaptique(voir wikipedia):

import numpy as np
def perceptron(X, y, max_iterations=1000):
"""
Implémente l'algorithme du perceptron avec un biais négatif.
:param X: Matrice de caractéristiques (n échantillons, d caractéristiques)
:param y: Vecteur des labels (-1 ou 1)
:param max_iterations: Nombre maximal d'itérations pour éviter une boucle infinie
:return: Vecteur de poids W
"""
n_samples, n_features = X.shape
print(f"Number of samples: {n_samples}, Number of features: {n_features}")
W = np.zeros(n_features + 1) # Initialisation du vecteur de poids avec biais
print("Initial W:", W)
X = np.c_[-np.ones(n_samples), X] # Ajout de la colonne de biais avec -1
print("Modified X:", X)
for _ in range(max_iterations):
error_count = 0
for i in range(n_samples):
if y[i] * np.dot(W, X[i]) <= 0:
W += y[i] * X[i]
error_count += 1
if error_count == 0:
break # Arrête si aucune erreur
return W
# Exemple d'utilisation
data = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
labels = np.array([-1, 1, 1, 1]) # Labels pour la porte OR
W_final = perceptron(data, labels)
print("Poids finaux:", W_final)
Poids finaux: [1. 2. 2.]
